现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回

归的假设函数在计算什么。

在逻辑回归中，我们预测：

当ℎ?(?) >= 0.5时，预测 ? = 1。

当ℎ?(?) < 0.5时，预测 ? = 0 。

根据上面绘制出的 S 形函数图像，我们知道当

? = 0 时 ?(?) = 0.5

? > 0 时 ?(?) > 0.5

? < 0 时 ?(?) < 0.5

又 ? = ??? ，即：

??? >= 0 时，预测 ? = 1

??? < 0 时，预测 ? = 0

现在假设我们有一个模型：

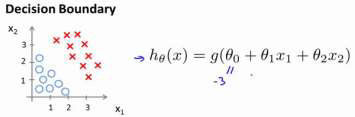
　　并且参数? 是向量[-3 1 1]。 则当−3 + ?1 + ?2 ≥ 0，即?1 + ?2 ≥ 3时，模型将预测 ? =

1。 我们可以绘制直线?1 + ?2 = 3，这条线便是我们模型的分界线，将预测为1 的区域和预

测为 0 的区域分隔开。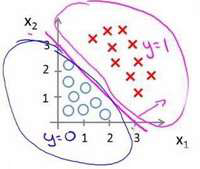

假使我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

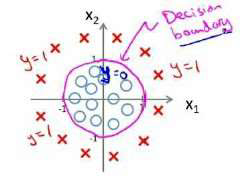
　　因为需要用曲线才能分隔 ? = 0 的区域和 ? = 1 的区域，我们需要二次方特征：

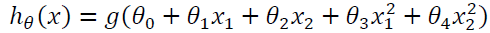
是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆

点在原点且半径为1 的圆形。

我们可以用非常复杂的模型来适应非常复杂形状的判定边界。